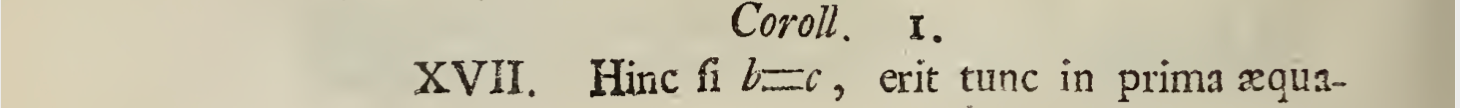September 11, 2020

De integraionibus aequationum differentialium

Bernoulli Title

On the integration of differential equations

Where an example of a method of integrating without earlier separation of variables is recounted.

Author Johann Beroulli, June 1726

Bernoulli 1 Bernoulli 1_2

1.

When any first degree differential equation has been reduced to $p dx = q dy$ , ubi $p$ datur per $x$ , & $q$ per $y$ , that is, in my manner of speaking, ubi $p$ & $q$ are any functions given by the indeterminates $x$ & $y$ ; in this case, the construction of the equation poses no difficulty, (including of course second order equations); which can be generalized to extensions of algebraic curves which were not first reduced, see Cel. Hermanni’s article in Acta Eruditorum of Liepzig, 1723. I also treated this analytic material in the same journal’s 1724 publication.

To go in this way in no

utpote === namely, as , since

Bernoulli 2

2.

Moreover, if because the differential equation $p dx = q dy$ is produced with mixed indeterminates, that is, if both quantities $p$ & $q$ or one of the two at least are diversely composed of the indeterminates $x$ & $y$ simultaneously, and of these different powers, or containing or not containing different radical signs; it indeed is

hūcusque (not comparable) === up to this point, until now

Bernoulli 3 Bernoulli 3_2

3.

Given particular rules, even if all cases in which are generally applicable, which are applied.

Marquis de l’Hôpital,

Bernoulli 4

4.

Bernoulli 5 Bernoulli 5_2

5.

Bernoulli 6 Bernoulli 6_2

6.

Bernoulli 7 Bernoulli 7_2 Bernoulli 7_3

7.

Bernoulli 8 Bernoulli 8_2

8.

Bernoulli 9

9.

I proceed to the method invented by myself to the integratino of differential equations without the use of separation of indeterminates, any of them in another transmutation made by substitution; I say here of these equations $p d x + q d y = 0$ , in which $p$ & $q$ indicate rational, homogeneous functions of the indeterminates $x$ & $y$ however between them complicated and mingled, only the indeterminates in every end having the same exponent, because these functions, of which are so prepared, these very differential equations which are composed of these I call homogeneous.